Evo još nekih metoda za prognozu ranih jesenjih i kasnih prolećnih mrazeva. Izvor je Marko Milosavljević - Klimatologija. U nekom od prethodnih postova sam naveo da je to Meteorologija, ali eto, živ čovek, pa greši. Nema veze, važno je da je još tih metoda tu, i da će biti dostupni i na ovaj način.
Prognoza pomoću temperature tačke rose i temperature vazduhaU ovom slučaju odredi se temperatura tačka rose i to prethodnog dana oko 17 časova. ako je temperatura tačke rose ispod 0°C, minimum temperature u nastupajućoj noći neće pasti ispod 0°C. Ako je temperatura tačke rose samo malo iznad 0°C (na primer 0.5°c), ipak se mora računati sa izvesnom opasnošću od mraza za osetljive biljke.
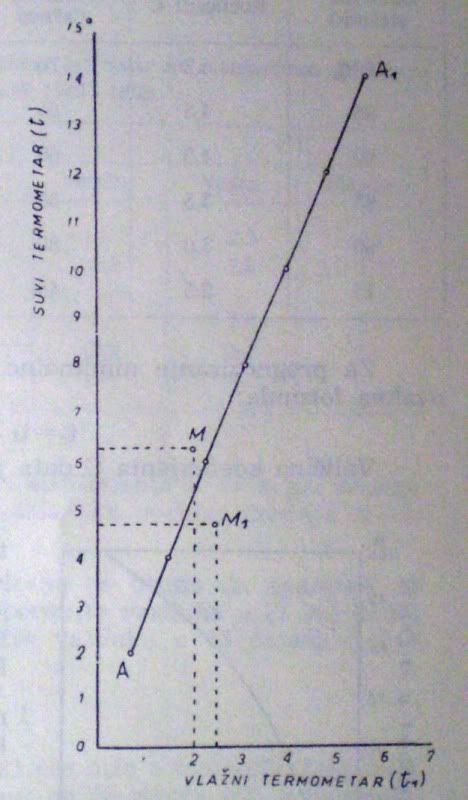
Langovo praviloPo ovom pravilu, opasnost od mraza postoji ako je u 17 časova mokri termometar bio niži od suvog, i to:
- pri temperaturi od 14°C, ako je razlika između suvog i mokrog termometra bila veća od 5.8°C,
- pri temperaturi od 12°C, ako je razlika između suvog i mokrog termometra bila veća od 4.9°C,
- pri temperaturi od 10°C, ako je razlika između suvog i mokrog termometra bila veća od 4.0°C,
- pri temperaturi od 8°C, ako je razlika između suvog i mokrog termometra bila veća od 3.1°C,
- pri temperaturi od 6°C, ako je razlika između suvog i mokrog termometra bila veća od 2.3°C,
- pri temperaturi od 4°C, ako je razlika između suvog i mokrog termometra bila veća od 1.5°C,
- pri temperaturi od 2°C, ako je razlika između suvog i mokrog termometra bila veća od 0.7°C
Ovo pravilo se može predstaviti i grafički:
 Prognoziranje noćnog mraza po formuli Mihaljevskog
Prognoziranje noćnog mraza po formuli MihaljevskogZa prognoziranje nastupajućeg noćnog mraza Mihaljevski daje sledeću formulu:
Tmin = Tm - (T - Tm) x C
Ovde je:
Tmin - minimalna temperatura koja se prognozira
Tm - temperatura mokrog termometra u 13 časova prethodnog dana
T - temperatura vazduha u 13 časova prethodnog dana
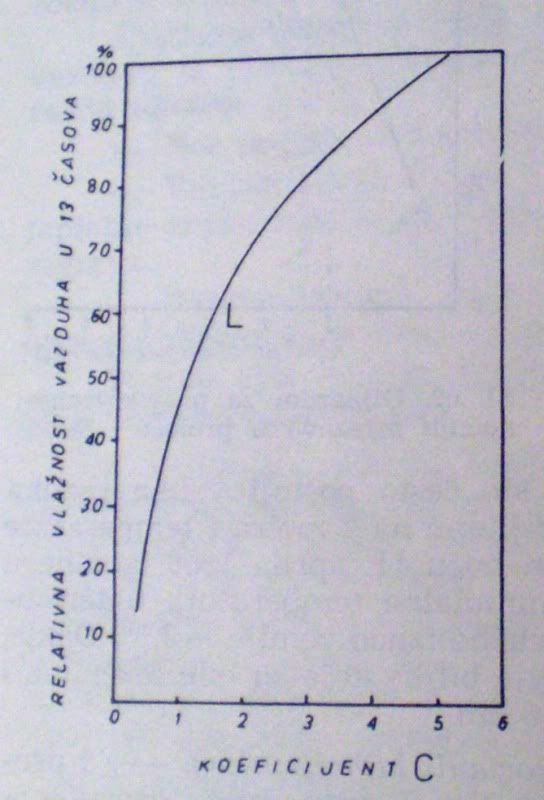
C - koeficijent koji zavisi od vlažnosti vazduha.
Koeficijent C ima sledeće vrednosti:
- pri relativnoj vlažnosti 100% koeficijent ima vrednost 5.2
- pri relativnoj vlažnosti 95% koeficijent ima vrednost 4.5
- pri relativnoj vlažnosti 90% koeficijent ima vrednost 4.0
- pri relativnoj vlažnosti 85% koeficijent ima vrednost 3.5
- pri relativnoj vlažnosti 80% koeficijent ima vrednost 3.0
- pri relativnoj vlažnosti 75% koeficijent ima vrednost 2.5
- pri relativnoj vlažnosti 70% koeficijent ima vrednost 2.0
- pri relativnoj vlažnosti 65% koeficijent ima vrednost 1.8
- pri relativnoj vlažnosti 60% koeficijent ima vrednost 1.5
- pri relativnoj vlažnosti 55% koeficijent ima vrednost 1.3
- pri relativnoj vlažnosti 50% koeficijent ima vrednost 1.2
- pri relativnoj vlažnosti 45% koeficijent ima vrednost 1.0
- pri relativnoj vlažnosti 40% koeficijent ima vrednost 0.9
- pri relativnoj vlažnosti 35% koeficijent ima vrednost 0.8
- pri relativnoj vlažnosti 30% koeficijent ima vrednost 0.7
- pri relativnoj vlažnosti 25% koeficijent ima vrednost 0.5
- pri relativnoj vlažnosti 20% koeficijent ima vrednost 0.4
- pri relativnoj vlažnosti 15% koeficijent ima vrednost 0.3
Zavisnost vrednosti ovog koeficijenta od relativne vlažnosti vazduha se može predstaviti i sledećim grafikom:
 Korostelov metod
Korostelov metodPrema ovom metodu pretpostavlja se da je razlika između temperature mokrog termometra u 21 čas i minimalne temperature vazduha u narednoj noći dovoljno postojana veličina, pa se može pidati da je
Tmin = Tm - K
gde je K koeficijent koji treba odrediti za svako mesto, jer zavisi od lokalnih karakteristika kretanja temperature na datoj stanici.
Za stanicu u Radmilovcu (kod Vinče) ovi koeficijenti su određeni iz perioda osmatranja 1949-1958, po mesecima, za vedro i za oblačno vreme posebno. Evo vrednosti koeficijenta K u ovom primeru:
Mart, III dekada: za vedro vreme 2.3, za oblačno vreme 2.2
April, I dekada: za vedro vreme 2.7, za oblačno vreme 2.5
April, II dekada: za vedro vreme 3.2, za oblačno vreme 2.7
April, III dekada: za vedro vreme 2.5, za oblačno vreme 2.3
Maj, I dekada: za vedro vreme 2.1, za oblačno vreme 1.8
Septembar, III dekada: za vedro vreme 2.8, za oblačno vreme 2.8
Oktobar, I dekada: za vedro vreme 2.7, za oblačno vreme 2.1
Oktobar, II dekada: za vedro vreme 2.8, za oblačno vreme 2.2
Oktobar, III dekada: za vedro vreme 2.4, za oblačno vreme 2.3
Novembar, I dekada: za vedro vreme 2.1, za oblačno vreme 2.0
Braunov metodPrema ovom metodu, verovatnoća pojave mraza zavisi od temperature vazduha u 21 čas početkom noći i razlike između temperatura u 13 i 21 čas. Dakle,
dT = T
13 - T
21Za određivanje verovatnoće pojave mraza po ovom metodu koristi se ovaj grafikon:
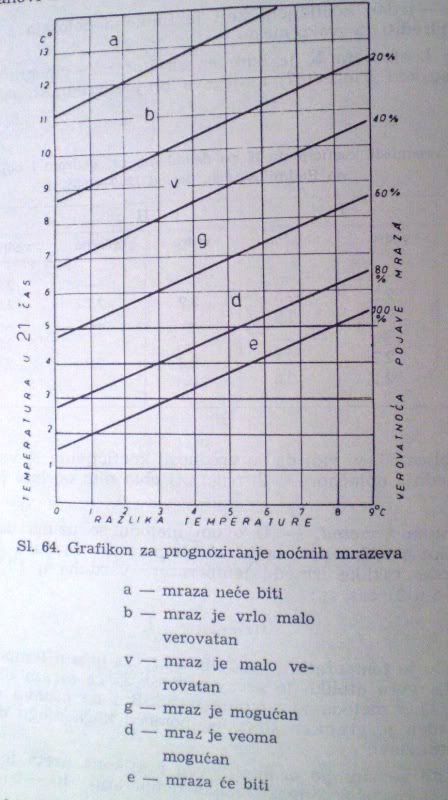
Ako volite da se zanimate za mrazeve, ima dovoljno metoda koji su bili korišćeni za prognozu pojave mraza. Izvol'te, služite se! I javite rezultate.